Mathematical Paradoxes : by Komal

Komal MSc. Mathematics

Mathematical paradoxes have fascinated mathematicians, philosophers, and curious minds for centuries. They offer seemingly impossible situations or counterintuitive outcomes that challenge our understanding of the world. In this post, we’ll explore three of the most famous paradoxes: Zeno’s Paradoxes, the Monty Hall Problem, and the Banach-Tarski Paradox. These paradoxes reveal deep insights into the nature of infinity, probability, and geometry, all while offering surprising solutions that defy our everyday intuition.

Zeno’s Paradoxes: The Infinite and the Finite
Zeno of Elea, a Greek philosopher, introduced several paradoxes that appeared to show that motion was impossible and just a mere illusion. These paradoxes seemed to prove that the idea of motion or change is flawed.
Let’s focus on two of the most famous paradoxes: Achilles and the Tortoise and The Arrow Paradox.
Achilles and the Tortoise Paradox
Imagine that the swift Achilles is racing a tortoise. Achilles runs ten times faster than the tortoise, and we give the tortoise a 10-meter head start. Zeno argues that Achilles will never catch the tortoise. Here's why:
- Every time Achilles reaches the point where the tortoise started, the tortoise has moved a little further ahead.
- Even though Achilles is faster, there are infinitely many small steps he must take to close the gap, leading Zeno to conclude that motion is impossible.
The Resolution: Calculus and Limits
While this paradox baffled philosophers for centuries, modern mathematics has resolved it through calculus. Zeno’s argument relied on the idea of infinitely dividing time and space. Today, we understand that although there are infinitely many steps, the sum of these steps can still be finite.
In mathematical terms, this is a converging infinite series. The total distance Achilles runs is a geometric series that sums to a finite value.
Calculus teaches us that while the number of steps is infinite, the time it takes for Achilles to overtake the tortoise is finite.

Example: If Achilles runs 10 times faster than the tortoise, and the tortoise starts 10 meters ahead, we can express the total distance Achilles runs as:

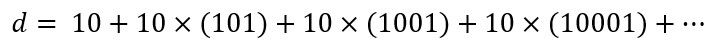
The sum of an infinite geometric series is given by the formula:

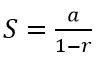
where:

a is the first term,
r is the common ratio

For our series:

a = 10
r = 1/10

So, the sum is:

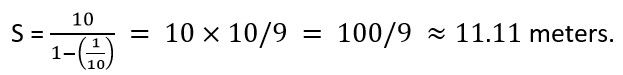
So, Achilles does indeed catch the tortoise after covering a total distance of just over 11 meters.

2. The Monty Hall Problem: Probability and Intuition

The Monty Hall Problem is one of the most famous paradoxes in probability theory. It’s based on a game show scenario where you have to choose one of three doors, behind one of which is a car and behind the other two, goats. Monty, the host, knows where the car is, and after you make your choice, he opens one of the other doors to reveal a goat. He then offers you the chance to switch your choice to the remaining door. The question is: Should you switch or stay with your original choice?

Intuition vs. Reality

At first glance, it seems like you have a 50-50 chance of winning if you switch or stay. After all, two doors remain, right? However, the correct strategy is to always switch. By switching, your probability of winning the car increases to 2/3, while staying gives you only a 1/3 chance.

The Mathematical Explanation

Here’s why the strategy of switching works:

1. Initial Choice: When you pick a door, there’s a 1/3 chance that the car is behind your chosen door and a 2/3 chance that it’s behind one of the other two doors.

2. Monty’s Action: Monty always reveals a goat behind one of the remaining doors, so his action gives you additional information.

3. Switching: After Monty opens a door, the 2/3 chance that the car is behind one of the other doors is transferred to the remaining door. So, switching gives you a 2/3 chance of winning, while sticking with your original choice leaves you with only a 1/3 chance.

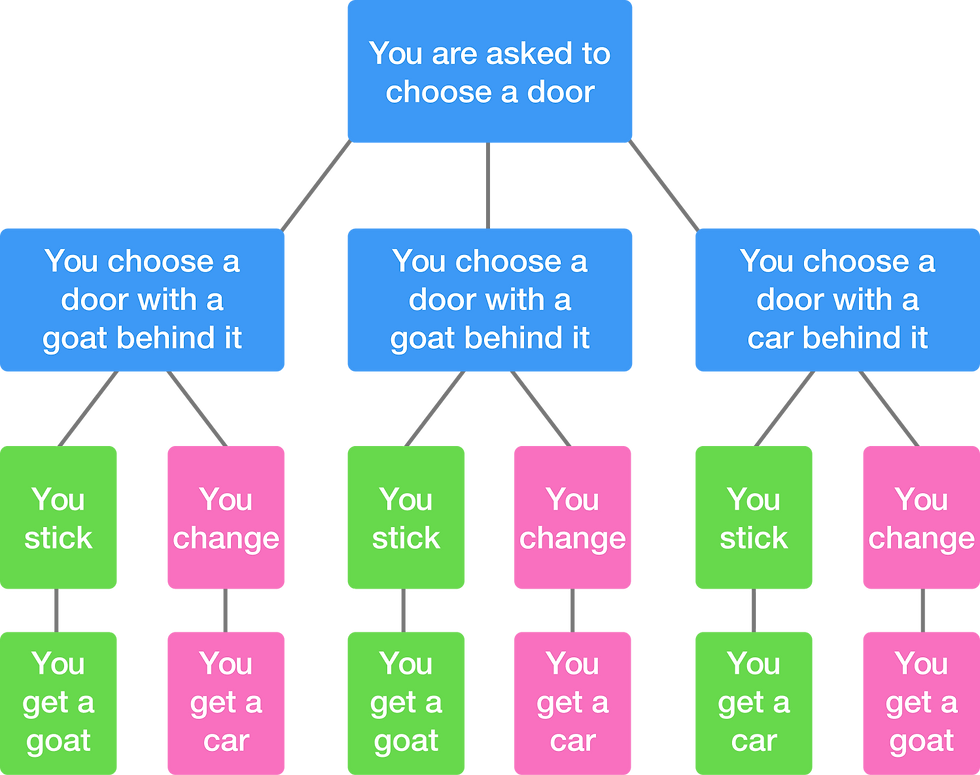
A Simulated Example:

If you simulate the game 1,000 times, you’ll find that switching wins approximately 667 times, while staying wins only about 333 times. This clear difference underscores how probability works in this situation, and why our intuition can sometimes be wrong.

3. The Banach-Tarski Paradox: The Infinite Splitting of Space

The Banach-Tarski Paradox is one of the most bizarre results in mathematics, and it challenges our understanding of space and geometry. It states that it’s possible to take a solid sphere, break it into a finite number of pieces, and reassemble those pieces into two identical copies of the original sphere. This result is highly counterintuitive and relies on concepts from set theory and infinity.

What’s Going On?

The Banach-Tarski Paradox uses the Axiom of Choice, a controversial principle in set theory that allows you to choose elements from an infinite number of sets, even when no specific rule exists for making the choice. The paradox hinges on the fact that the pieces you end up with aren’t regular, measurable objects in the traditional sense—they are abstract mathematical sets with no well-defined size or shape.

How It Works:

1. Decomposition: The solid sphere is decomposed into a finite number of non-measurable pieces. These pieces can be arbitrarily strange and don’t resemble regular geometric shapes.

2. Reassembly: Using only rotations and translations (no stretching or shrinking), these pieces can be rearranged to form two identical copies of the original sphere.

Why It’s Mind-Boggling:

The paradox defies common sense because it suggests that space can be divided and reassembled in ways that violate our physical intuition. However, this doesn’t work in the real world, where objects are made of atoms and have physical constraints. The Banach-Tarski Paradox is purely theoretical and relies on the abstract manipulation of infinite sets.

Why Do These Paradoxes Matter?

Mathematical paradoxes are not just curiosities; they often reveal deeper truths about the world of mathematics and the nature of reality itself. Here’s why they are so important:

Zeno’s Paradoxes paved the way for calculus by illustrating the strange properties of infinite processes and the idea of limits.
The Monty Hall Problem demonstrates how probability doesn’t always align with intuition, offering insights into the counterintuitive nature of randomness.
The Banach-Tarski Paradox challenges our understanding of space, volume, and infinity, showing that our physical world doesn’t always mirror abstract mathematical concepts.

These paradoxes are not just interesting puzzles—they have profound implications for how we understand the universe through mathematics.

Reference: Wikipedia